What are the suitable measures to describe variability or spread in student scores
The Quartile Deviation
The concept of Range and its application have been discussed before. Let us now consider another measure of spread of student scores. This is the Quartile Deviation.
Consider a test to 18 BED (Com) students who scored the following marks and ranked from highest to the least score (Simplified example)
The first quartile is Q1 (lower), the second is Q2 (median) and, the upper quartile is Q3.
Therefore, the upper quartile is a point in a distribution below which 75% of scores lies-also referred as the 75th percentile and
The lower quartile is a point in a distribution below which 25% of the marks lie-also referred as the 25th percentile
Is half the difference between the UPPER quartile Q3 and LOWER quartile Q1
Which lead us to define Quartile Deviation (QD) = Q3 – Q1/2
The procedures for finding Q1 and Q3 is similar to that used for finding the Median in a distribution
The median is in fact the second Quartile Q2
N = number of scores (cases) in the distribution
cfb = commutative frequency below the interval containing the quartile.
fw= the frequency of scores (cases) within the interval containing the quartile.
i = the interval size.
If the value of the upper and lower quartile is a distribution are respectively 35 and 15, the value of QD = 35 -15/2
The quartile deviation belongs to the same statistics family as the median because it is an ordinal scale. It is sometimes called semi interquartile range.
It is not influenced by a few extreme scores (one very high or very low as it lies at 75th upper and 25 lower Example:
Quartile interpretation
If the Quartile deviation – QD for income of UDOM lecturer is Tshs 2,000,000 and that of St. Johns 1,500,000/= then we know the incomes of UDOM Staff is more heterogamous than that St. Johns, i.e. from the formula Q3-Q1/2, the interqurtile range for UDOM is higher!
Variance and standard deviation
Variance and Standard Deviation are the most us useful measures of variability or spread of scores
Both are based on deviations of scores from the mean, that is:
Deviations show the difference between a raw score and the mean
Raw scores below the mean will have negative deviations while,
Scores above the mean have positive deviations
The sum of the deviations scores is always ZERO!, represented by the symbol ᵟ-delta. The symbol is called delta. For simplicity we shall use the letter ‘d’. Example. If the scores of 5 students in a test are: 18, 20, 25, and 30 32 then the mean is: 18 + 32 +25 + 20 + 30/5= 25, i.e. sum of the deviations is d=(18-25) + (20 -25) + (25 – 25) + (30 – 25) + (32 – 25)= 0!
To get around this problem of getting the sum of zero, the technique is to SQUARE the deviations ‘d’ scores so that they will become positive numbers
The summation of the squared deviations divided by the number of scores we get the Mean of the squared deviations commonly known as VARIANCE
d2 or Variance= ∑ X2/N
The summation of the squared deviations divided by the number of scores we have the means squared deviations for the mean called the VARIANCE. In mathematical formula variance is
d2 = ∑X2 divide by N
Deviations
Explained as:
d2 = variance, ∑ = sum, (the symbol ∑ is called sigma)
x = deviation of each score from the mean
(X-X) = x otherwise know as deviation scores
N = the number of scores in the deviation
Units of Variance
The resulting units is cm (squared)If for example in the end we have 4cm2 and another groups 2cm2 we may say the first group is more heterogeneous (more scattered) than the group with 2cm2 variance.
Consider the following example
Standard deviation (SD)
The basic procedures is therefore
i. Find the mean
ii. Find the squares of the difference between raw score and the mean
iii. Find the square root to obtain the Standard Deviation (SD) often represented by the symbol, now we shall be using the symbol ‘d’ for simplicity
The standard scores
Sometimes we may be interested in finding the distance of certain score from the mean. This distance is called Z – Score as measured by the standard deviation and is given by:
Z (score) = X - X = xi/d, Where
X = the raw score
X = the mean of the distribution
d= SD
xi = the deviation scores (X – X)
This may help us to compare how far is a certain score from the mean in say two subjects. Consider the following example:
Z-scores in two subjects.
Suppose now the scores in the same two subjects is 81 (psychology) and 53 (SE 301) and the same mean and standard deviations which tests has the students done better?
To show this we use the same formula
(We use the same formula)
To solve this complication we very often use another standard score which have no negative numbers or decimals.
The most common measure is the T-score distribution, commonly known as the standard score
The T-Score
Example
Suppose the student score test is 21 and, the mean in that test is 27 while the standard deviation is 6. What is the Standardized score? We proceed as follows
Z - score = 21 – 27 divide by 6
Then the standardized score T-score of this student is:
T = 50 + 10 (21 – 27) /6
= 40 - this is higher than the previous score of 21!
What does all these arithmetical calculations mean?
i. Teachers who wish to compare the standings of their student on successive tests can convert the student's raw score to Z-scores then standardize of to T-score!
ii. Teachers who wish to compare the standings of their student, may standardize the scores by considering the scores obtained on different tests in the same course. That is, can convert the student raw marks to T-scores in order to give equal weight to each set of scores.
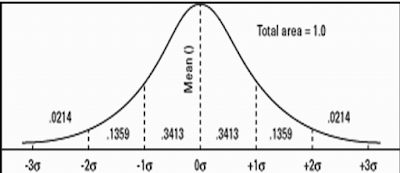
The normal curve
Research and experience reveal that the distribution of many measures (if randomly selected) take the shape of a bell when plotted on a frequency distribution table: Examples
Height of BAED, BED SC, B.Sc. Ed in UDOM
Weight of BAED, BED SC, B.SC ED and so on
A polygon showing this distribution closely resembles a theoretical polygon known as the normal curve.
What are the features of a normal curve?
Shows a symmetrical distribution of scores below and above the mean (equal)
Its mean divide the measures into two halves (50% above the mean and the other 50% below the mean)
The mean median and mode fall on the same point (coincide)
In a normal curve, most of the measures concentrate around the mean
The frequency of the cases decreases as we proceed away from the mean is either direction
A proximately 34%, fall above and below the mean and the distribution decreases evenly above and below the mean.
To this point we have been dealing with measures of central tendencies (clustering around the mean ) and variability (dispersion, spread). We may be interested on other statistical relationships. Let us see important ones.
Correlations relationships
Why study correlations? The interest in correlations is on the need to indicate the relationship between pairs of certain variables. What is it? Height and basketball ability, nutrition and survival, entrepreneur mentality and job creation, education and diseases and so on.
Statistical technique for determining the relationships between pairs of variables known also as correlation procedures
The purpose is to determine if there is a relationship between paired measurements
Shows the extent to which change in one variable is associated with change in another variable but NOT the cause!
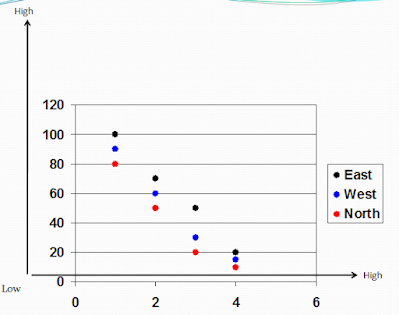
It can generally be assumed that intelligent students achieve high in classroom tests. We may consider for example to see the correlation between Intelligence Quotient (IQ a ratio of mental age to chronological age) and test scores. A scattergram is obtained.
The relationship is that there is a tendency for achievement Scores to be high when the cognitive ability is high (see graph)
Scattergram help us to see both the direction and strength of the relationship
Direction and strength of the relationship is positive or negative.
For the above scatter gram, the correlation is positive
It is possible to associate high score and high intelligence (see scattergram)
Scores of the independent variable x are plotted along the horizontal axis and scores of the dependent variable y are plotted on the vertical axis.
Correlations or relationships are not always positive.
Think of birthrate and income for example of people.
Correlation Coefficients
These are statistical measures (indexes) which shows whether the relationship or correlation is negative or positive.
Shows also the strength between variables of choice (think of the intelligence and achievement, economic status and birth rate, education and development, honest and hooliganism, education and diseases also forth.
Calculations of correlations coefficient between two variables have values between -1.00 and +1.00 and the interpretation is
What does a correlation -1.00 mean?
It means a perfect negative relationship for example that of income and birthrate
What about a correlation of +1.00?
Shows a perfect positive relationship for example parents education and pupil achievement in school. Can you give other examples?
Shows no relationship at all between the variables. For example tribe and achievement in school! another example?
What does a correlation at the midpoint mean?
Shows no relationship
That is, no relationship at all between the variables
What does a correlation close to 1.00 or +1.00 mean? The impression is that it is close to perfect relationship. Further explanation is given next.
Indicate very high negative relationship high relationship allow accurate prediction (If this is what data analysis indicate about one variable on the basis of the other).
A negative correlation is just as good a prediction as positive correlation
Think of the following scatter gram about correlations between two arbitrary variables. State whether perfect positive, perfect negative. High positive, high negative, moderate, zero correlation and soon.
You may have discovered that when the relationship between variables is perfectly positive or negative all the scores fall on a straight line score
For zero relationships, the scores are just scattered over the surface of the graph and do not take any shape in any direction
Correlation coefficients in educational research (measures) seldom reach a maximum points of +1.00 and -1.00
For this kind of correlation coefficient that is greater than plus or minus 0.90 is usually considered very high (conventional).
The product moment correlation or sometimes called Pearson ‘r’ (from the English statistician Karl Pearson.). Product multiplication of two variables
Interpretation of the Pearson r
N = The number of paired scores. When two variables are highly related in a positive way. The correlations between approaches +1. When in a negative way, the correlation approaches -1
When there is no relationship between variables, the correlation will be near O (zero) direction of relationship
Person r indicate a meaningful index (measure) for indicating relationship with the sign of coefficient indicating the direction of relationship
Caution on interpretation of the correlation coefficient
a) Correlation does not necessarily indicate the cause. It just shows the association between the two variables.
It does not mean changes in one variable are caused by changes in the other variables.
Correlation coefficient may tell us that a person with above average score on one test will probably obtain an above average score on the other test but we cannot say a high performance on one test causes high performance on the other.
Scores of both tests may result from other causes such as numerical understanding of the person who teach the test.
b) The sizes of the correlation is function of the variability of the two distributions
Depend on the size of the sample with reasonable variation.
That is restricting the range of the scores to be correlated reduces the observed degree of relationship between two variables.
Example. Success in playing basketball is related to height. The taller the individual, the better he can play or succeed.
This is true if we take a wide range of heights. It may not hold if you take a few who are already tall.
c) Correlation coefficient not interpreted in term of percentage
This is seen when for example ‘r’ of +0.80 does not indicate 80% perfect relationship between two variables.
This relationship is not correct because for example a is ‘r’ of + 0.80 does not express a relationship that is twice as great as an ‘r’ of + 0.40
d) Avoid interpreting the coefficients of correlation in an absolute sense
We have to keep in mind the purpose for which the correlation is to be used.
+0.50 so may be satisfactory if we thinking of performance of individual in future task but not to perform surgical tasks.
Meta Analysis
A method for a systematically combining quantitative data from a number of studies focusing on the same question and using similar variables
Studies comparing groups that got treatment (experimental group) with groups that did not get treatment (control group)
In doing so, one clearness a common metric that is interpreted as an overall summary of outcomes for the selected studies.
For each study the difference between control and experimental mean is translated into standard deviation units by dividing this difference by the SD of the control group.
This ratio is SD units is labeled as effect size.
Effect size averages interpreted as the best estimate of the direction and magnitude of the effect of the independent variable on the dependent variable.
Meta studies can be used not only with studies that compare means but also with studies of correlation proportion and other measures.































Post a Comment